About Me

I am a researcher in numerical linear algebra and connected fields at Charles University in Prague ("Karlín" building, office 464 at the fourth floor).

My interest in mathematics began in my family with my granduncle Prof. Jiří Outrata and was further developed by my undergraduate supervisors Prof. Zdeněk Strakoš (bachelor) and Prof. Miroslav Tůma (master). During that time I also completed an internship at the University of Bath with Dr. James Hook and Prof. Alasatir Spence.

During the final year of my master's studies, I asked for and was offered a PhD position with Prof. Martin Gander at the University of Geneva and I have been thrilled to collaborate with him ever since, successfully defendeding my PhD thesis in Decembre 2022. Our research project has been awarded and supported by the Swiss Government Excellence Scholarship for three years (maximum possible). I was also awarded the Henri Fehr Prize for the best PhD thesis in mathematics in 2023 and wrote a short summary of the research.

Moving forward, I was offered and completed a postdoc position at Virginia Tech with Prof. Eric de Sturler as my mentor, taking advantage of consulting with all of the members of the strong applied mathematics group at Virginia Tech.

As of the fall of 2024, I am starting at the position of assistant professor at Charles Univresity Numerical Mathematics Department. Recently, I have been awarded the Primus Research Programme grant and I'm very much looking forward to taking full advantage of the opportunities this opens up both for me and my to-be-assembled team (see the "Research" tab for open positions).

Skills and Languages

•   Czech (native)   •   English (fluent)   •   French (conversational)   •   German (passive)   •
•   Python   •   Matlab   •   LaTeX   •   Jupyter   •  

CV

Available upon request.

Research

My research & collaborations   •   Primus Programme (2025-2028)   •   ORCiD   •   GitHub

Generally speaking, I'm interested in understanding why certain numerical methods (usually iterative) work for some classes of problems the way they do. So the emphasis is not primarily on proposing new algorithms but rather understanding really well the existing ones. However, as a byproduct, we often find out the existing ones can be improved on, leading to new methods nonetheless.

Current team members: PostDocs

Current team members: Bachelor level

  • Eva Fóglová
  • Jiří Harvalík

If you are thinking about a collaboration with me and/or my team that's great! Stop by my office or write me an email and we'll set up a (online) meeting to discuss your interests.

My research & collaborations

Krylov methods   •   Domain decomposition methods   •   Others

Krylov methods

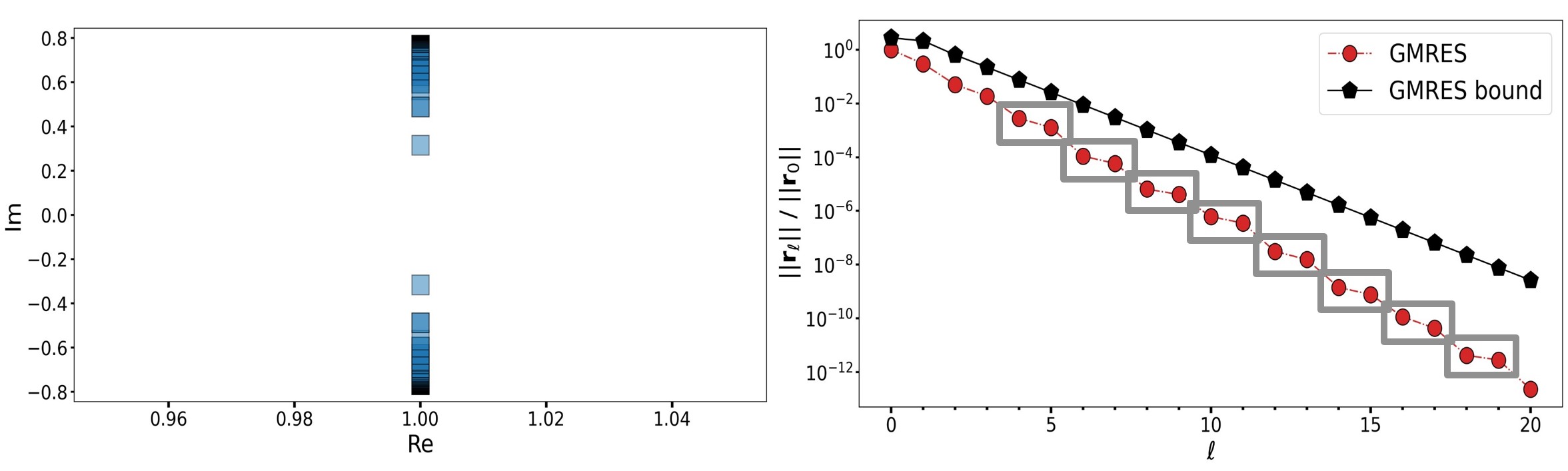
I've worked with and on Krylov methods both in Prague and Geneva. My first topic of interest was GMRES and its convergence behavior and eventually became my Bachelor thesis topic, under the supervision of Prof. Zdeněk Strakoš. The work was an (incomplete) overview of the deep results about GMRES convergence behavior and we finished by looking on polynomial methods in general on infinite-dimensional spaces and in what sense we should think about the approximations of the solution and the operators when we discretize and use a Krylov method, e.g., GMRES. As a result, I obtained a solid theoretical background in theory and analysis of Krylov methods and GMRES in particular.

I continued to be interested in these methods and worked on a preconditioner for CG in my Master thesis with Prof. Miroslav Tůma. We focused on problems where the system matrix is dually sparse. In particular we considered a block matrix with general rectangular block structure such that considerable amount of the blocks are zero and a lot of the non-zero ones are data-sparse (i.e., either low-rank or well-approximable by some hierarchical format). As a result, I learned techniques to deal both with structurally sparse matrices (elimination tree, graph prunning, ...) as well as with the data-sparse ones, e.g., hierarchical formats (such as HODLR, H, ...) but also low-rank approximation techniques (CUR approximation, randomized techniques, ...).

With Prof. Martin Gander we have looked at the newly proposed block GMRES preconditioner for systems coming out of implicit Runge-Kutta discretizations of paraboplic PDEs - originaly the work of Prof. Victoria Howle and her group. We tried to understand why does this family of preconditioners perform the way it does and obtained some non-trivial understanding and analysis. Recently, I have started a collaboration with them and I'm very much looking forward to it. If you are interested in this line of work, I would also recommend looking at the work of Ivo Dravins and his collaboratos - we worked on a very similar problem independently arriving at very closely related results only from a different angles.

With Prof. Eric de Sturler we have been working on preconditioner maps that allow us to recycle preconditioners in an efficient way for sequnce of linear problems, using data-sparsity and hierarchical matrix formats.

Domain decomposition methods methods

During my PhD I've transitioned to domain decomposition methods and the Schwarz methods in particular, navigated by Prof. Martin Gander. We started with optimized Schwarz methods withdata-sparse transmission conditions as a natural progression given my Master's background. This topic turned out to be very challenging to analyze, especially in contrast to structurally sparse transmission conditions. However the numerical results are very promising for the standard model problems. This naturally lead to further study of convergence behavior and convergence bounds in particular for the algebraic formulations of Schwarz methods.

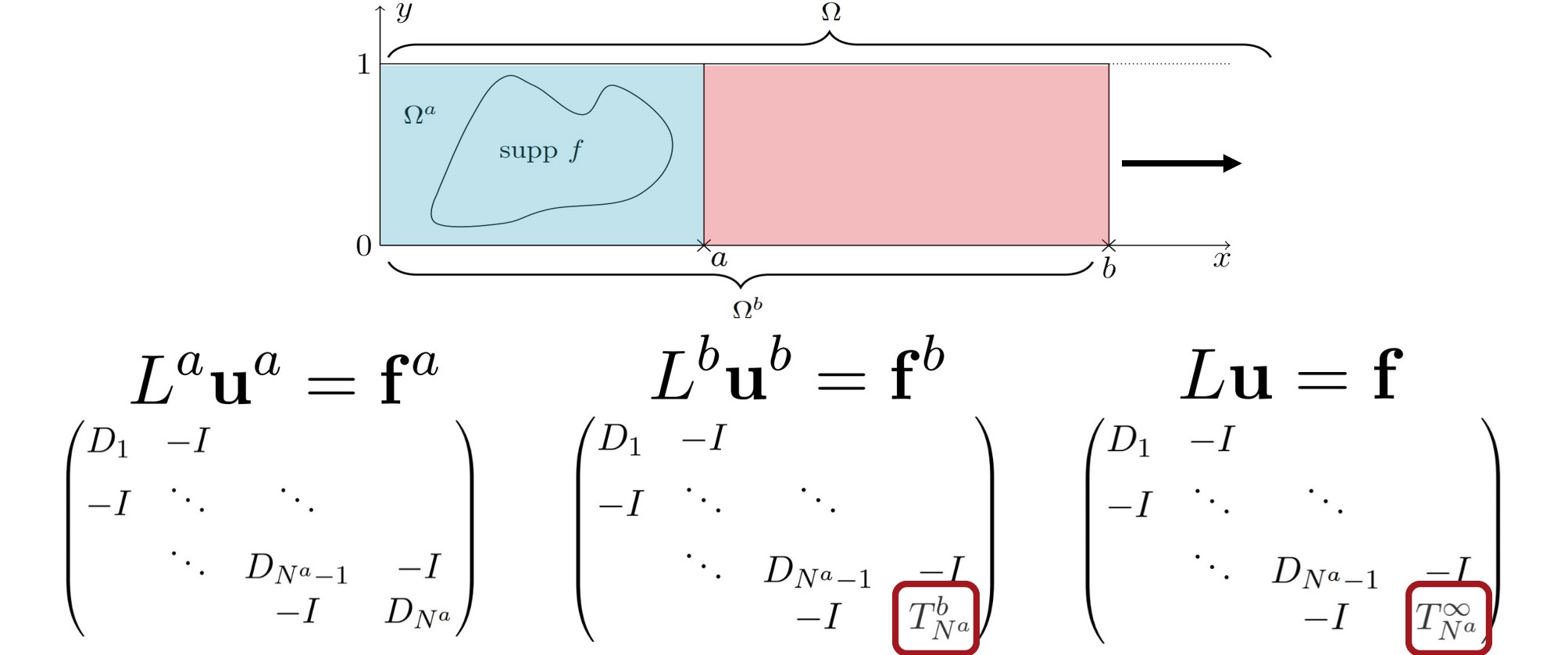
With Prof. Martin Gander and Lukáš Jakabčin we worked on Schur complement approximation qualities, focusing on the Schur complement on a truncated mesh and its relation to the Schur complement on unbounded domain. In practice, this work is analogous to studying perfectly matched layers (and the closely related absorbing boundary conditions), thus relating to DD methods in general. For a simple academical problem, we were able to prove that prolonging the boundary layer corresponds to increasing the degree of a certain Pade approximation, using continued fraction techniques and representations.

Other

Me and my granduncle Jiří Outrata have done some research in set-valued convex optimization but I deviated from this line of research already during my bachelor studies in Prague.

Primus Research Programme

General info   •   Open PostDoc positions   •   Open PhD positions   •   Results

General info

Project name

Divide, Conquer and Optimize: Domain Decomposition Methods in Scientific Computing

Project duration: Jan 2025 - Dec 2028
Place: Department of Numerical Mathematics, Faculty of Mathematics and Physics, Charles University, Prague, Czech republic
Project PI: Michal Outrata
Our team
  • We are looking to establish one before the project takes off.
Project annotation

Solving systems of linear equations is ubiquitous in scientific computing and its efficiency often acts as the bottleneck of the entire computation, making the idea of domain decomposition methods (DDM) attractive. Using DDM, we decompose the system into smaller ones (subdomain problems) and introduce an iterative scheme (a DDM) that solves these iteratively while exchanging information after each iteration (see [this paper]). Hence, a key question for any DDM is what information should be exchanged so that the iterative scheme converges.
The first focal point of this project is to give a faithful mathematical model of DDM performance for specific types of information exchange techniques, involving hierarchical matrix formats (see [these lecture notes]) and/or mixed precision computations (see [this paper]). These models will allow us to optimize these techniques and we will study the efficiency, robustness and applicability of the resulting optimized DDM (see [this paper]).
The second one is to expand this model to the situation where we accelerate DDM with a Krylov subspace method (see [this book]) so that the method itself adapts from iteration to iteration based on its progress.

Open positions: PostDoc

The offer

The appointment period is two years, with a possible extension for an extra year. The Postdoc will start early in 2025, with the precise date being negotiable. The project offers an international environment at one of the top universities in Czech republic and the oldest university in Central Europe. Additionally, the project also involves collaboration with international experts from Switzerland and the US and includes a travel funding for presenting our results at conferences and meetings. The position's salary is sufficient to ensure a comfortable life in Prague.

The candidates profile

We are looking for candidates with a strong background in numerical linear algebra and numerical analysis. In particular, we seek applicants with expertise in (a) iterative methods for solution of large linear systems with applications to differential equations (ideally domain decomposition methods or Krylov subspace methods) or (b) hierarchical matrix computations and analysis or (c) mixed precision computations. Solid command of a programming language of choice (python, MATLAB, C/C++, julia, ...) is a necessity. Good English writing and speaking skills are required. The applicant must hold a Ph.D. degree by the starting date.

Application
  • Curriculum Vitae
  • Cover Letter explaining motivation and interests with regards to the project
  • List of publications
  • Up to a 1 page Research statement (describing your research interests and results so far, including figures)
  • The Ph.D. thesis (if not available, please get in touch before submitting the application)
  • Two letters of recommendation, sent by their authors to the same email address before the same deadline

The application should be sent to outrata@karlin.mff.cuni.cz
If you're not sure if you're interested and/or fit well - just write and ask and we can have a (zoom) meeting to discuss things in more detail :).

Open positions: PhD

The offer

The PhD studies arte expected to take around 4 years, with a possible extension (also depending on ongoing funding). The ideal start date is in fall 2025 but negotiable. The project offers an international environment at one of the top universities in Czech republic and the oldest university in Central Europe. Additionally, the project also involves collaboration with international experts from Switzerland and the US and includes a travel funding for presenting our results at conferences and meetings. The position's salary together with the PhD stipend should be sufficient to have a nice life in Prague.

The candidates profile

We are looking for candidates with a solid background in numerical linear algebra and/or numerical analysis. Ideally, the candidate should have experience with (a) iterative methods for solution of large linear systems with applications to differential equations (ideally domain decomposition methods or Krylov subspace methods) or (b) hierarchical matrix computations and analysis or (c) mixed precision computations. Being comfortable with a programming language of choice (python, MATLAB, C/C++, julia, ...) is a necessity. Good English writing and speaking skills are required. The applicant must hold a Master's degree degree by the starting date and will have to formally enroll in the PhD program at Charles University.

Application
  • Curriculum Vitae
  • Cover Letter explaining motivation and interests with regards to the project
  • Up to a 1 page Research statement (describing your research interests and results so far, including figures)
  • The pdf file of the Master's thesis (if not available, please get in touch before submitting the application)
  • A letter of recommendation, sent by its author to the same email address before the same deadline

The application should be sent to outrata@karlin.mff.cuni.cz
If you're not sure if you're interested and/or fit well - just write and ask and we can have a (zoom) meeting to discuss things in more detail :).

Results

More to come here soon.

Talks and Conferences

Manuscripts and Preprints

Journal Publications   •   Conference Proceedings   •   In Preparation   •   How To Cite

Peer-reviewed Journal Publications

Peer-reviewed Conference Proceedings

In preparation

How to cite

For your convenience, I'm posting the references for the above I am currently (depending on the last update) using: the bib items.

Teaching & supervising

Most of my teaching experience has been truly positive and pleasant. As a teaching assistent (TA) I was in charge (not necessarily solely) of preparing and presenting the exercises (often heavily inspired by previous runs of the course) and/or correcting these and giving feedback to students. As a lecturer (L) I was in charge of teaching the course as well as organizing the course. For these courses I created the assignments and assessments from scratch (but, of course, relying on the existing literature) and was grading these during the semesdter and exam periods.

If you are interested in working on a Bachelor/Master project together, I would love for you to come and visit me in my office and/or write me an email about it. Any topic you are interested in is a good one!

Current teaching

Past teaching - Undergraduate level

  • Numerical Analysis
    • (cz) Charles University, Fall 2024 (TA for Doc. Iveta Hnětýnková & Doc. Václav Kučera; exercise notes)
    • (fr) University of Geneva, Fall 2020 - Fall 2023 (TA for Prof. Gilles Vilmart)
  • Introduction to Differential Equations
    • (en) Virginia Tech, Fall 2023, CRN 87176 (L)
    • (en) Virginia Tech, Fall 2023, CRN 92235 (L)
    • (en) Virginia Tech, Spring 2023, CRN 17316 (L)
  • Linear Algebra
    • (fr-en) University of Geneva, Fall 2019 (TA for Prof. Bart Vandereycken)
    • (cz) Charles University in Prague, Fall 2017 (TA for Prof. Libor Barto)
  • Calculus I
    • (fr-en) University of Geneva, Fall 2019 - Fall 2021 (TA for Prof. Pavol Ševera)
    • (cz) Prague University of Economics and Business, Fall 2016 - Fall 2017 (TA for Dr. Lukáš Krump)

Past teaching - Graduate level

  • Maxwell Equations and Scientific Computing
    • (fr-en) University of Geneva, Spring 2020 (TA for Prof. Martin Gander)
  • Low-rank Models in Scientific Simulation and Machine Learning
    • (en) University of Geneva, Fall 2019 (TA for Prof. Bart Vandereycken)

Úvod do numerické matematiky

Info ke kurzu   •   Týden 1   •   Týden 2   •   Týden 3   •   Týden 4   •   Týden 5   •   Týden 6   •   Týden 7   •   Týden 8   •   Týden 9   •   Týden 10   •   Týden 11   •   Týden 12   •   Týden 13

Intro

  • Konkretizace zkoušky pro praktickou a teoretickou část.
  • Udělení zápočtu a podmínky zkoušky jsou na SISu.
  • Body ze zápočtových kvízů tady.
  • Přidělení zápočtových projektů je tady.
  • Kvízy a simulace z přednášek jsou k nalezení (bez zdrojáku) tady.
  • Před prvním cvikem doporučuju si projít opáčko pythonu pro naše potřeby: cviko 0.

Týden 1

  • Poznámky k přednášce: P1 a P2 .
  • Na cvikách se bude dělat interpolace.
  • Hodnocený kvíz během tohohle týdne není, ale tady je cvičný kvíz, ať víte co čekat. Žádné body za něj nepřiděluju.

Týden 2

Týden 3

Týden 4

Týden 5

Týden 6

Týden 7

Týden 8

Týden 9

Týden 10

Týden 11

Týden 12

Týden 13

More about me

The goal of this page is for you (be it a student or a (potential) collaborator) to get some insight into what I am like outside the academia. If we meet at lunch (or elsewhere), we could talk about dozen of things completely unrelated to anything written below but maybe these can serve as humble suggestions.
Currently I'm living with my wife Lea in Prague in Czech republic. In my free time I like to do sport activities and outdoor/indoor climbing has been my preferred sport for some time now. I used to play florbal as a goalie back in highschool but also did some handball, baseball, basketball and (beach) volleyball and I take part in these whenever possible.
I enjoy following cultural and political issues and more general discussions about learning, thinking and mind, in all of which I have found the podcaster and philosopher Sam Harris extremely helpful and influential.
From time to time I relax playing games - either with Lea, our friends or on my own. Our/my favourite titles include Terra Mystica, Puerto Rico, Wingspan, Dominion, Magic The Gathering, Code Names and Dixit but also Stellaris, It Takes Two or Diablo 2. Me and Lea also like to read and watch together - we enjoyed the Dune and the Foundation books, the Wool sagas but we also spent hours watching The Office or Red Dwarf series or listening to the audiobooks of Terry Prachett.